Welcome to PyOD documentation!#

Deployment & Documentation & Stats & License

Read Me First#

Welcome to PyOD, a versatile Python library for detecting anomalies in multivariate data. Whether you’re tackling a small-scale project or large datasets, PyOD offers a range of algorithms to suit your needs.

For time-series outlier detection, please use TODS.
For graph outlier detection, please use PyGOD.
Performance Comparison & Datasets: We have a 45-page, the most comprehensive anomaly detection benchmark paper. The fully open-sourced ADBench compares 30 anomaly detection algorithms on 57 benchmark datasets.
Learn more about anomaly detection @ Anomaly Detection Resources
PyOD on Distributed Systems: you could also run PyOD on databricks.

About PyOD#

PyOD, established in 2017, has become a go-to Python library for detecting anomalous/outlying objects in multivariate data. This exciting yet challenging field is commonly referred as Outlier Detection or Anomaly Detection.

PyOD includes more than 50 detection algorithms, from classical LOF (SIGMOD 2000) to the cutting-edge ECOD and DIF (TKDE 2022 and 2023). Since 2017, PyOD has been successfully used in numerous academic researches and commercial products with more than 17 million downloads. It is also well acknowledged by the machine learning community with various dedicated posts/tutorials, including Analytics Vidhya, KDnuggets, and Towards Data Science.

PyOD is featured for:

Unified, User-Friendly Interface across various algorithms.
Wide Range of Models, from classic techniques to the latest deep learning methods.
High Performance & Efficiency, leveraging numba and joblib for JIT compilation and parallel processing.
Fast Training & Prediction, achieved through the SUOD framework [#Zhao2021SUOD]_.

Outlier Detection with 5 Lines of Code:

# Example: Training an ECOD detector
from pyod.models.ecod import ECOD
clf = ECOD()
clf.fit(X_train)
y_train_scores = clf.decision_scores_  # Outlier scores for training data
y_test_scores = clf.decision_function(X_test)  # Outlier scores for test data

Selecting the Right Algorithm:. Unsure where to start? Consider these robust and interpretable options:

ECOD: Example of using ECOD for outlier detection
Isolation Forest: Example of using Isolation Forest for outlier detection

Alternatively, explore MetaOD for a data-driven approach.

Citing PyOD:

PyOD paper is published in Journal of Machine Learning Research (JMLR) (MLOSS track). If you use PyOD in a scientific publication, we would appreciate citations to the following paper:

@article{zhao2019pyod,
    author  = {Zhao, Yue and Nasrullah, Zain and Li, Zheng},
    title   = {PyOD: A Python Toolbox for Scalable Outlier Detection},
    journal = {Journal of Machine Learning Research},
    year    = {2019},
    volume  = {20},
    number  = {96},
    pages   = {1-7},
    url     = {http://jmlr.org/papers/v20/19-011.html}
}

or:

Zhao, Y., Nasrullah, Z. and Li, Z., 2019. PyOD: A Python Toolbox for Scalable Outlier Detection. Journal of machine learning research (JMLR), 20(96), pp.1-7.

For a broader perspective on anomaly detection, see our NeurIPS papers ADBench: Anomaly Detection Benchmark & ADGym: Design Choices for Deep Anomaly Detection:

@article{han2022adbench,
    title={Adbench: Anomaly detection benchmark},
    author={Han, Songqiao and Hu, Xiyang and Huang, Hailiang and Jiang, Minqi and Zhao, Yue},
    journal={Advances in Neural Information Processing Systems},
    volume={35},
    pages={32142--32159},
    year={2022}
}

@article{jiang2023adgym,
    title={ADGym: Design Choices for Deep Anomaly Detection},
    author={Jiang, Minqi and Hou, Chaochuan and Zheng, Ao and Han, Songqiao and Huang, Hailiang and Wen, Qingsong and Hu, Xiyang and Zhao, Yue},
    journal={Advances in Neural Information Processing Systems},
    volume={36},
    year={2023}
}

ADBench Benchmark and Datasets#

We just released a 45-page, the most comprehensive ADBench: Anomaly Detection Benchmark [AHHH+22]. The fully open-sourced ADBench compares 30 anomaly detection algorithms on 57 benchmark datasets.

The organization of ADBench is provided below:

For a simpler visualization, we make the comparison of selected models via compare_all_models.py.

Implemented Algorithms#

PyOD toolkit consists of three major functional groups:

(i) Individual Detection Algorithms :

Type	Abbr	Algorithm	Year	Class	Ref
Probabilistic	ECOD	Unsupervised Outlier Detection Using Empirical Cumulative Distribution Functions	2022	`pyod.models.ecod.ECOD`	[ALZH+22]
Probabilistic	COPOD	COPOD: Copula-Based Outlier Detection	2020	`pyod.models.copod.COPOD`	[ALZB+20]
Probabilistic	ABOD	Angle-Based Outlier Detection	2008	`pyod.models.abod.ABOD`	[AKZ+08]
Probabilistic	FastABOD	Fast Angle-Based Outlier Detection using approximation	2008	`pyod.models.abod.ABOD`	[AKZ+08]
Probabilistic	MAD	Median Absolute Deviation (MAD)	1993	`pyod.models.mad.MAD`	[AIH93]
Probabilistic	SOS	Stochastic Outlier Selection	2012	`pyod.models.sos.SOS`	[AJHuszarPvdH12]
Probabilistic	QMCD	Quasi-Monte Carlo Discrepancy outlier detection	2001	`pyod.models.qmcd.QMCD`	[AFM01]
Probabilistic	KDE	Outlier Detection with Kernel Density Functions	2007	`pyod.models.kde.KDE`	[ALLP07]
Probabilistic	Sampling	Rapid distance-based outlier detection via sampling	2013	`pyod.models.sampling.Sampling`	[ASB13]
Probabilistic	GMM	Probabilistic Mixture Modeling for Outlier Analysis		`pyod.models.gmm.GMM`	[AAgg15] [Ch.2]
Linear Model	PCA	Principal Component Analysis (the sum of weighted projected distances to the eigenvector hyperplanes)	2003	`pyod.models.pca.PCA`	[ASCSC03]
Linear Model	KPCA	Kernel Principal Component Analysis	2007	`pyod.models.kpca.KPCA`	[AHof07]
Linear Model	MCD	Minimum Covariance Determinant (use the mahalanobis distances as the outlier scores)	1999	`pyod.models.mcd.MCD`	[AHR04, ARD99]
Linear Model	CD	Use Cook’s distance for outlier detection	1977	`pyod.models.cd.CD`	[ACoo77]
Linear Model	OCSVM	One-Class Support Vector Machines	2001	`pyod.models.ocsvm.OCSVM`	[AScholkopfPST+01]
Linear Model	LMDD	Deviation-based Outlier Detection (LMDD)	1996	`pyod.models.lmdd.LMDD`	[AAAR96]
Proximity-Based	LOF	Local Outlier Factor	2000	`pyod.models.lof.LOF`	[ABKNS00]
Proximity-Based	COF	Connectivity-Based Outlier Factor	2002	`pyod.models.cof.COF`	[ATCFC02]
Proximity-Based	Incr. COF	Memory Efficient Connectivity-Based Outlier Factor (slower but reduce storage complexity)	2002	`pyod.models.cof.COF`	[ATCFC02]
Proximity-Based	CBLOF	Clustering-Based Local Outlier Factor	2003	`pyod.models.cblof.CBLOF`	[AHXD03]
Proximity-Based	LOCI	LOCI: Fast outlier detection using the local correlation integral	2003	`pyod.models.loci.LOCI`	[APKGF03]
Proximity-Based	HBOS	Histogram-based Outlier Score	2012	`pyod.models.hbos.HBOS`	[AGD12]
Proximity-Based	kNN	k Nearest Neighbors (use the distance to the kth nearest neighbor as the outlier score	2000	`pyod.models.knn.KNN`	[AAP02, ARRS00]
Proximity-Based	AvgKNN	Average kNN (use the average distance to k nearest neighbors as the outlier score)	2002	`pyod.models.knn.KNN`	[AAP02, ARRS00]
Proximity-Based	MedKNN	Median kNN (use the median distance to k nearest neighbors as the outlier score)	2002	`pyod.models.knn.KNN`	[AAP02, ARRS00]
Proximity-Based	SOD	Subspace Outlier Detection	2009	`pyod.models.sod.SOD`	[AKKrogerSZ09]
Proximity-Based	ROD	Rotation-based Outlier Detection	2020	`pyod.models.rod.ROD`	[AABC20]
Outlier Ensembles	IForest	Isolation Forest	2008	`pyod.models.iforest.IForest`	[ALTZ08, ALTZ12]
Outlier Ensembles	INNE	Isolation-based Anomaly Detection Using Nearest-Neighbor Ensembles	2018	`pyod.models.inne.INNE`	[ABTA+18]
Outlier Ensembles	DIF	Deep Isolation Forest for Anomaly Detection	2023	`pyod.models.dif.DIF`	[]
Outlier Ensembles	FB	Feature Bagging	2005	`pyod.models.feature_bagging.FeatureBagging`	[ALK05]
Outlier Ensembles	LSCP	LSCP: Locally Selective Combination of Parallel Outlier Ensembles	2019	`pyod.models.lscp.LSCP`	[AZNHL19]
Outlier Ensembles	XGBOD	Extreme Boosting Based Outlier Detection (Supervised)	2018	`pyod.models.xgbod.XGBOD`	[AZH18]
Outlier Ensembles	LODA	Lightweight On-line Detector of Anomalies	2016	`pyod.models.loda.LODA`	[APevny16]
Outlier Ensembles	SUOD	SUOD: Accelerating Large-scale Unsupervised Heterogeneous Outlier Detection (Acceleration)	2021	`pyod.models.suod.SUOD`	[AZHC+21]
Neural Networks	AutoEncoder	Fully connected AutoEncoder (use reconstruction error as the outlier score)	2015	`pyod.models.auto_encoder.AutoEncoder`	[AAgg15] [Ch.3]
Neural Networks	VAE	Variational AutoEncoder (use reconstruction error as the outlier score)	2013	`pyod.models.vae.VAE`	[AKW13]
Neural Networks	Beta-VAE	Variational AutoEncoder (all customized loss term by varying gamma and capacity)	2018	`pyod.models.vae.VAE`	[ABHP+18]
Neural Networks	SO_GAAL	Single-Objective Generative Adversarial Active Learning	2019	`pyod.models.so_gaal.SO_GAAL`	[ALLZ+19]
Neural Networks	MO_GAAL	Multiple-Objective Generative Adversarial Active Learning	2019	`pyod.models.mo_gaal.MO_GAAL`	[ALLZ+19]
Neural Networks	DeepSVDD	Deep One-Class Classification	2018	`pyod.models.deep_svdd.DeepSVDD`	[ARVG+18]
Neural Networks	AnoGAN	Anomaly Detection with Generative Adversarial Networks	2017	`pyod.models.anogan.AnoGAN`	[ASSeebockW+17]
Neural Networks	ALAD	Adversarially learned anomaly detection	2018	`pyod.models.alad.ALAD`	[AZRF+18]
Graph-based	R-Graph	Outlier detection by R-graph	2017	`pyod.models.rgraph.RGraph`	[BYRV17]
Graph-based	LUNAR	LUNAR: Unifying Local Outlier Detection Methods via Graph Neural Networks	2022	`pyod.models.lunar.LUNAR`	[AGHNN22]

(ii) Outlier Ensembles & Outlier Detector Combination Frameworks:

Type	Abbr	Algorithm	Year	Ref
Outlier Ensembles		Feature Bagging	2005	`pyod.models.feature_bagging.FeatureBagging`	[ALK05]
Outlier Ensembles	LSCP	LSCP: Locally Selective Combination of Parallel Outlier Ensembles	2019	`pyod.models.lscp.LSCP`	[AZNHL19]
Outlier Ensembles	XGBOD	Extreme Boosting Based Outlier Detection (Supervised)	2018	`pyod.models.xgbod.XGBOD`	[AZH18]
Outlier Ensembles	LODA	Lightweight On-line Detector of Anomalies	2016	`pyod.models.loda.LODA`	[APevny16]
Outlier Ensembles	SUOD	SUOD: Accelerating Large-scale Unsupervised Heterogeneous Outlier Detection (Acceleration)	2021	`pyod.models.suod.SUOD`	[AZHC+21]
Combination	Average	Simple combination by averaging the scores	2015	`pyod.models.combination.average()`	[AAS15]
Combination	Weighted Average	Simple combination by averaging the scores with detector weights	2015	`pyod.models.combination.average()`	[AAS15]
Combination	Maximization	Simple combination by taking the maximum scores	2015	`pyod.models.combination.maximization()`	[AAS15]
Combination	AOM	Average of Maximum	2015	`pyod.models.combination.aom()`	[AAS15]
Combination	MOA	Maximum of Average	2015	`pyod.models.combination.moa()`	[AAS15]
Combination	Median	Simple combination by taking the median of the scores	2015	`pyod.models.combination.median()`	[AAS15]
Combination	majority Vote	Simple combination by taking the majority vote of the labels (weights can be used)	2015	`pyod.models.combination.majority_vote()`	[AAS15]

(iii) Utility Functions:

Type	Name	Function
Data	`pyod.utils.data.generate_data()`	Synthesized data generation; normal data is generated by a multivariate Gaussian and outliers are generated by a uniform distribution
Data	`pyod.utils.data.generate_data_clusters()`	Synthesized data generation in clusters; more complex data patterns can be created with multiple clusters
Stat	`pyod.utils.stat_models.wpearsonr()`	Calculate the weighted Pearson correlation of two samples
Utility	`pyod.utils.utility.get_label_n()`	Turn raw outlier scores into binary labels by assign 1 to top n outlier scores
Utility	`pyod.utils.utility.precision_n_scores()`	calculate precision @ rank n

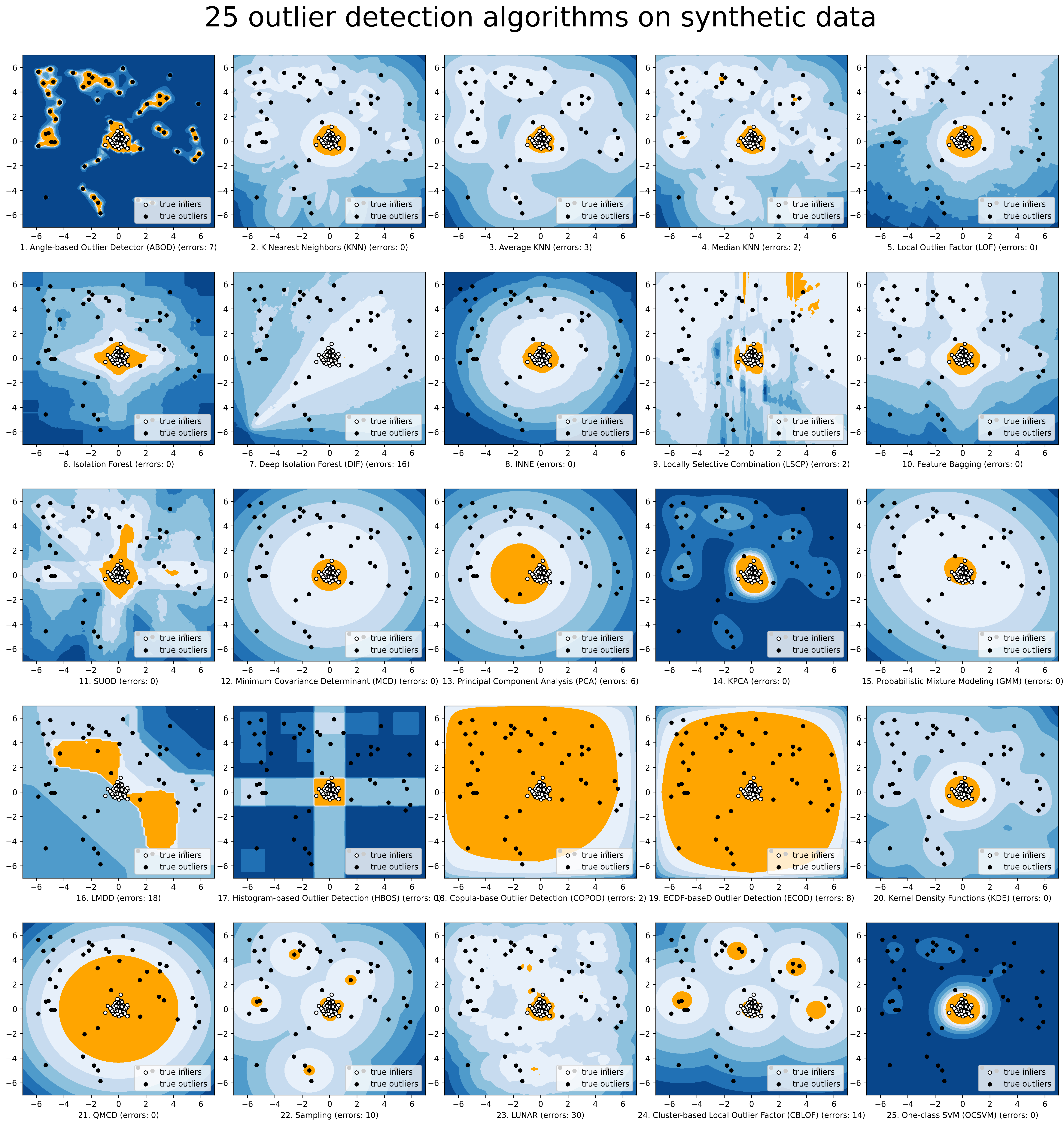
The comparison among of implemented models is made available below (Figure, compare_all_models.py, Interactive Jupyter Notebooks). For Jupyter Notebooks, please navigate to “/notebooks/Compare All Models.ipynb”.

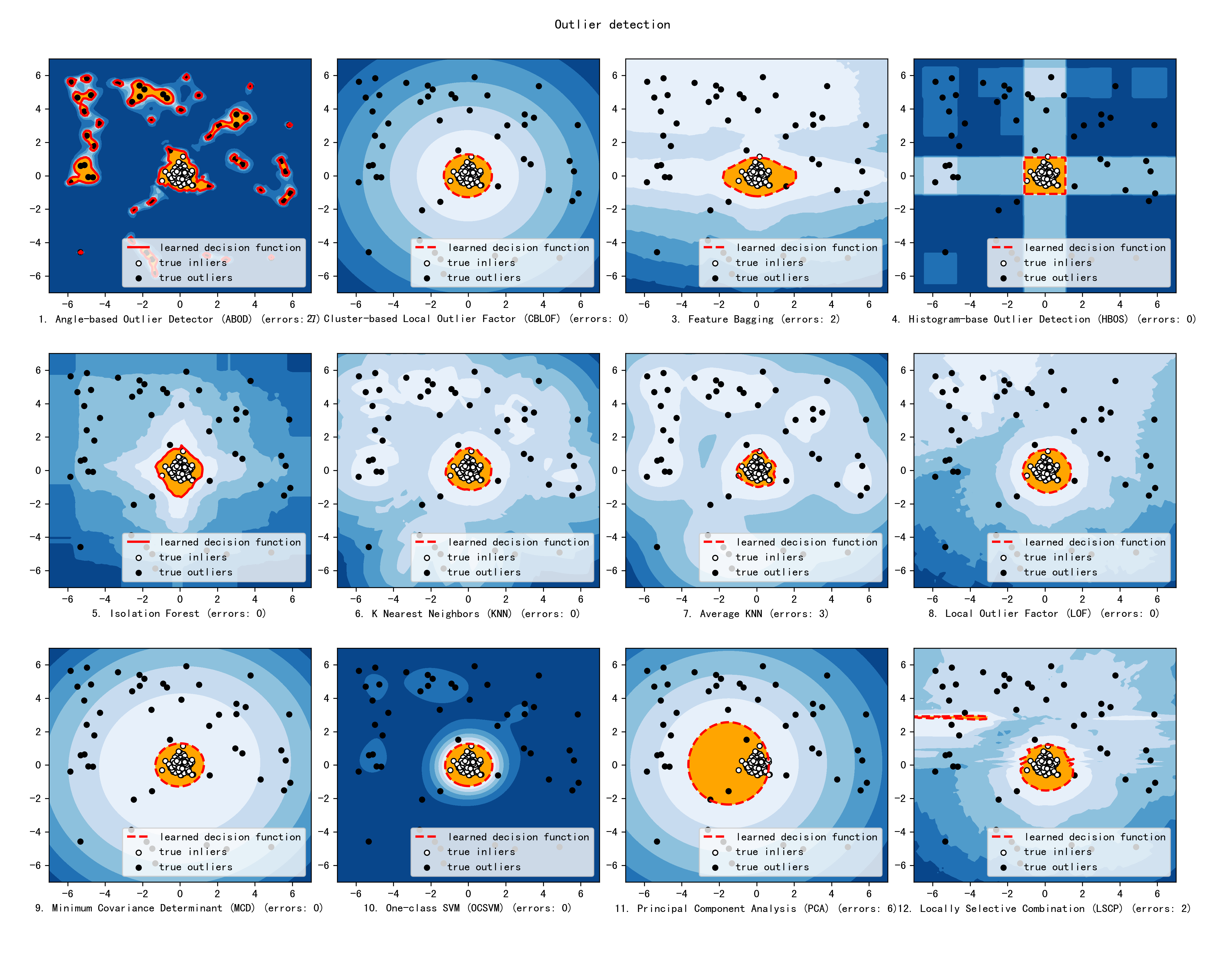
Check the latest benchmark. You could replicate this process by running benchmark.py.

API Cheatsheet & Reference#

The following APIs are applicable for all detector models for easy use.

pyod.models.base.BaseDetector.fit(): Fit detector. y is ignored in unsupervised methods.
pyod.models.base.BaseDetector.decision_function(): Predict raw anomaly score of X using the fitted detector.
pyod.models.base.BaseDetector.predict(): Predict if a particular sample is an outlier or not using the fitted detector.
pyod.models.base.BaseDetector.predict_proba(): Predict the probability of a sample being outlier using the fitted detector.
pyod.models.base.BaseDetector.predict_confidence(): Predict the model’s sample-wise confidence (available in predict and predict_proba).

Key Attributes of a fitted model:

pyod.models.base.BaseDetector.decision_scores_: The outlier scores of the training data. The higher, the more abnormal. Outliers tend to have higher scores.
pyod.models.base.BaseDetector.labels_: The binary labels of the training data. 0 stands for inliers and 1 for outliers/anomalies.

References

[AAgg15] (1,2)

Charu C Aggarwal. Outlier analysis. In Data mining, 75–79. Springer, 2015.

[AAS15] (1,2,3,4,5,6,7)

Charu C Aggarwal and Saket Sathe. Theoretical foundations and algorithms for outlier ensembles. ACM SIGKDD Explorations Newsletter, 17(1):24–47, 2015.

[AABC20]

Yahya Almardeny, Noureddine Boujnah, and Frances Cleary. A novel outlier detection method for multivariate data. IEEE Transactions on Knowledge and Data Engineering, 2020.

[AAP02] (1,2,3)

Fabrizio Angiulli and Clara Pizzuti. Fast outlier detection in high dimensional spaces. In European Conference on Principles of Data Mining and Knowledge Discovery, 15–27. Springer, 2002.

[AAAR96]

Andreas Arning, Rakesh Agrawal, and Prabhakar Raghavan. A linear method for deviation detection in large databases. In KDD, volume 1141, 972–981. 1996.

[ABTA+18]

Tharindu R Bandaragoda, Kai Ming Ting, David Albrecht, Fei Tony Liu, Ye Zhu, and Jonathan R Wells. Isolation-based anomaly detection using nearest-neighbor ensembles. Computational Intelligence, 34(4):968–998, 2018.

[ABKNS00]

Markus M Breunig, Hans-Peter Kriegel, Raymond T Ng, and Jörg Sander. Lof: identifying density-based local outliers. In ACM sigmod record, volume 29, 93–104. ACM, 2000.

[ABHP+18]

Christopher P Burgess, Irina Higgins, Arka Pal, Loic Matthey, Nick Watters, Guillaume Desjardins, and Alexander Lerchner. Understanding disentangling in betvae. arXiv preprint arXiv:1804.03599, 2018.

[ACoo77]

R Dennis Cook. Detection of influential observation in linear regression. Technometrics, 19(1):15–18, 1977.

[AFM01]

Kai-Tai Fang and Chang-Xing Ma. Wrap-around l2-discrepancy of random sampling, latin hypercube and uniform designs. Journal of complexity, 17(4):608–624, 2001.

[AGD12]

Markus Goldstein and Andreas Dengel. Histogram-based outlier score (hbos): a fast unsupervised anomaly detection algorithm. KI-2012: Poster and Demo Track, pages 59–63, 2012.

[AGHNN22]

Adam Goodge, Bryan Hooi, See-Kiong Ng, and Wee Siong Ng. Lunar: unifying local outlier detection methods via graph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 36, 6737–6745. 2022.

[AHHH+22]

Songqiao Han, Xiyang Hu, Hailiang Huang, Mingqi Jiang, and Yue Zhao. Adbench: anomaly detection benchmark. arXiv preprint arXiv:2206.09426, 2022.

[AHR04]

Johanna Hardin and David M Rocke. Outlier detection in the multiple cluster setting using the minimum covariance determinant estimator. Computational Statistics & Data Analysis, 44(4):625–638, 2004.

[AHXD03]

Zengyou He, Xiaofei Xu, and Shengchun Deng. Discovering cluster-based local outliers. Pattern Recognition Letters, 24(9-10):1641–1650, 2003.

[AHof07]

Heiko Hoffmann. Kernel pca for novelty detection. Pattern recognition, 40(3):863–874, 2007.

[AIH93]

Boris Iglewicz and David Caster Hoaglin. How to detect and handle outliers. Volume 16. Asq Press, 1993.

[AJHuszarPvdH12]

JHM Janssens, Ferenc Huszár, EO Postma, and HJ van den Herik. Stochastic outlier selection. Technical Report, Technical report TiCC TR 2012-001, Tilburg University, Tilburg Center for Cognition and Communication, Tilburg, The Netherlands, 2012.

[AKW13]

Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.

[AKKrogerSZ09]

Hans-Peter Kriegel, Peer Kröger, Erich Schubert, and Arthur Zimek. Outlier detection in axis-parallel subspaces of high dimensional data. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, 831–838. Springer, 2009.

[AKZ+08] (1,2)

Hans-Peter Kriegel, Arthur Zimek, and others. Angle-based outlier detection in high-dimensional data. In Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining, 444–452. ACM, 2008.

[ALLP07]

Longin Jan Latecki, Aleksandar Lazarevic, and Dragoljub Pokrajac. Outlier detection with kernel density functions. In International Workshop on Machine Learning and Data Mining in Pattern Recognition, 61–75. Springer, 2007.

[ALK05] (1,2)

Aleksandar Lazarevic and Vipin Kumar. Feature bagging for outlier detection. In Proceedings of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining, 157–166. ACM, 2005.

[ALZB+20]

Zheng Li, Yue Zhao, Nicola Botta, Cezar Ionescu, and Xiyang Hu. COPOD: copula-based outlier detection. In IEEE International Conference on Data Mining (ICDM). IEEE, 2020.

[ALZH+22]

Zheng Li, Yue Zhao, Xiyang Hu, Nicola Botta, Cezar Ionescu, and H. George Chen. Ecod: unsupervised outlier detection using empirical cumulative distribution functions. IEEE Transactions on Knowledge and Data Engineering, 2022.

[ALTZ08]

Fei Tony Liu, Kai Ming Ting, and Zhi-Hua Zhou. Isolation forest. In Data Mining, 2008. ICDM'08. Eighth IEEE International Conference on, 413–422. IEEE, 2008.

[ALTZ12]

Fei Tony Liu, Kai Ming Ting, and Zhi-Hua Zhou. Isolation-based anomaly detection. ACM Transactions on Knowledge Discovery from Data (TKDD), 6(1):3, 2012.

[ALLZ+19] (1,2)

Yezheng Liu, Zhe Li, Chong Zhou, Yuanchun Jiang, Jianshan Sun, Meng Wang, and Xiangnan He. Generative adversarial active learning for unsupervised outlier detection. IEEE Transactions on Knowledge and Data Engineering, 2019.

[APKGF03]

Spiros Papadimitriou, Hiroyuki Kitagawa, Phillip B Gibbons, and Christos Faloutsos. Loci: fast outlier detection using the local correlation integral. In Data Engineering, 2003. Proceedings. 19th International Conference on, 315–326. IEEE, 2003.

[APevny16] (1,2)

Tomáš Pevn\`y. Loda: lightweight on-line detector of anomalies. Machine Learning, 102(2):275–304, 2016.

[ARRS00] (1,2,3)

Sridhar Ramaswamy, Rajeev Rastogi, and Kyuseok Shim. Efficient algorithms for mining outliers from large data sets. In ACM Sigmod Record, volume 29, 427–438. ACM, 2000.

[ARD99]

Peter J Rousseeuw and Katrien Van Driessen. A fast algorithm for the minimum covariance determinant estimator. Technometrics, 41(3):212–223, 1999.

[ARVG+18]

Lukas Ruff, Robert Vandermeulen, Nico Görnitz, Lucas Deecke, Shoaib Siddiqui, Alexander Binder, Emmanuel Müller, and Marius Kloft. Deep one-class classification. International conference on machine learning, 2018.

[ASSeebockW+17]

Thomas Schlegl, Philipp Seeböck, Sebastian M Waldstein, Ursula Schmidt-Erfurth, and Georg Langs. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In International conference on information processing in medical imaging, 146–157. Springer, 2017.

[AScholkopfPST+01]

Bernhard Schölkopf, John C Platt, John Shawe-Taylor, Alex J Smola, and Robert C Williamson. Estimating the support of a high-dimensional distribution. Neural computation, 13(7):1443–1471, 2001.

[ASCSC03]

Mei-Ling Shyu, Shu-Ching Chen, Kanoksri Sarinnapakorn, and LiWu Chang. A novel anomaly detection scheme based on principal component classifier. Technical Report, MIAMI UNIV CORAL GABLES FL DEPT OF ELECTRICAL AND COMPUTER ENGINEERING, 2003.

[ASB13]

Mahito Sugiyama and Karsten Borgwardt. Rapid distance-based outlier detection via sampling. Advances in neural information processing systems, 2013.

[ATCFC02] (1,2)

Jian Tang, Zhixiang Chen, Ada Wai-Chee Fu, and David W Cheung. Enhancing effectiveness of outlier detections for low density patterns. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, 535–548. Springer, 2002.

[AZRF+18]

Houssam Zenati, Manon Romain, Chuan-Sheng Foo, Bruno Lecouat, and Vijay Chandrasekhar. Adversarially learned anomaly detection. In 2018 IEEE International conference on data mining (ICDM), 727–736. IEEE, 2018.

[AZH18] (1,2)

Yue Zhao and Maciej K Hryniewicki. Xgbod: improving supervised outlier detection with unsupervised representation learning. In International Joint Conference on Neural Networks (IJCNN). IEEE, 2018.

[AZHC+21] (1,2)

Yue Zhao, Xiyang Hu, Cheng Cheng, Cong Wang, Changlin Wan, Wen Wang, Jianing Yang, Haoping Bai, Zheng Li, Cao Xiao, Yunlong Wang, Zhi Qiao, Jimeng Sun, and Leman Akoglu. Suod: accelerating large-scale unsupervised heterogeneous outlier detection. Proceedings of Machine Learning and Systems, 2021.

[AZNHL19] (1,2)

Yue Zhao, Zain Nasrullah, Maciej K Hryniewicki, and Zheng Li. LSCP: locally selective combination in parallel outlier ensembles. In Proceedings of the 2019 SIAM International Conference on Data Mining, SDM 2019, 585–593. Calgary, Canada, May 2019. SIAM. URL: https://doi.org/10.1137/1.9781611975673.66, doi:10.1137/1.9781611975673.66.